History and Hermeneutics for Mathematics
Education
Storia
ed Ermeneutica per la Didattica della Matematica
Lettres by Euler (1787)
Le Lettere di Eulero (1787)
Euler, L. (1787), Lettere ad una principessa d’Alemagna sopra diversi soggetti di Fisica e di
Filosofia, I, II, III, Ferres, Napoli (I ed. in Italian, II ed.; I ed.:
1772)
EULER Leonhard, lat. EULERUS (1707-1783)
“Per esprimere
sensibilmente la natura di queste quattro spezie di proposizioni, possiam
rappresentarle per mezzo di figure, le quali son di un gran soccorso per
ispiegare con somma distinzione qual sia l’esattezza di un raziocinio. E poiché
una nozione generale contiene un’infinità di oggetti individuali, si può
supporre a guisa di uno spazio, in cui questi oggetti son racchiusi: per
esempio si forma uno spazio per la nozione di uomo (Tav. 1. fig. 1.) in
cui si suppone che tutti gli uomini sien radunati.
Tav.
1. fig. 1.
Per la nozione di mortale se ne forma un altro (Tav.
1. fig. 2.) dove si suppone che sia compreso quanto vi è di mortale.
Tav.
1. fig. 2.
E quando io pronunzio che tutti gli uomini son mortali, intendo
che la prima figura sia contenuta nella seconda.
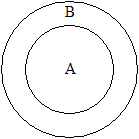
Tav.
1. fig. 3.
Dunque la rappresentazione di una
proposizione universale affermativa sarà quella della Tav. 1. fig. 3., in cui lo spazio A che dinota il soggetto della
proposizione vien tutto intero racchiuso nello spazio B che è il predicato”
(lettera CII, 14 febbraio 1761, II, pp. 111-112).
“Questi cerchj o sien questi spazj
(imperciocché è indifferente qualunque figura lor si dia) son molto a portata per
facilitare le nostre riflessioni sopra questa materia, e per metterci in chiaro
quanti misteri la logica si vanta di avere, i quali somma pena han costata per
poterli dimostrare, mentre coll’ajuto di tai segni in un istante tutto salta
agli occhi... Quanto sin qui si è detto può essere sufficiente a far capire a
Vostra Altezza , che tutte le proposizioni possono essere rappresentate con
figure; ma il massimo vantaggio si manifesta ne’ raziocinj, i quali qualora si
esprimon con parole chiamansi sillogismi,
in cui si tratta di tirare una conclusione esatta da alcune date proposizioni.
Con tale invenzione noi potremo subito scandagliare le giuste forme di tutti i
sillogismi.
Cominciamo da una proposizione
affermativa universale ogni A è B...
Se
Ogni
A è B
Ma Ogni C è A
Dunque Ogni C è B
e quest’ultima
è la conclusione
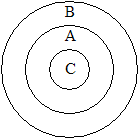
Tav.
1. fig. 8.
Per esempio. Disegni
Ogni
arbore ha radici
Ma Ogni ciriegio è un arbore
Dunque Ogni ciriegio ha radici”
(lettera CIII,
17 febbraio 1761, II, pp. 113 e 115-116).
Divisibilità dell’estensione in infinito
“La
controversia tra i Filosofi moderni, e i Geometri, di cui ora ho l’onore di parlare
a Vostra Altezza, ha per oggetto la divisibilità de’ corpi. Una tal proprietà è
senza dubbio fondata sull’estensione, e non per altro i corpi son divisibili e
posson ridursi in parti, se non perché sono estesi.
Si ricorderà benissimo Vostra Altezza,
che in Geometria si può sempre dividere una linea in due parti uguali, per
picciola che sia. S’insegna benanche il come debba dividersi una piccola linea,
per esempio a i in tante parti uguali
quante si vuole, e la costruzione di tal divisione vien talmente dimostrata che
non si può dubitar della sua esattezza.
Tav.
II. fig. 23
Non hassi a far altro che tirare (Tav. II. fig. 23.) una linea A I parallela ad a i a qualunque grandezza
ed a qualunque distanza si voglia, ed in essa trasportarvi altrettante porzioni
uguali AB, BC, CD, DE quante la picciola linea data
contiene, per esempio otto. Quindi per l’estremità Aa, ed Ii descrivansi le
linee rette AaO e IiO finché non arrivino al punto O: e da questo stesso punto O verso i punti di divisione B, C,
D, E, &c. tirinsi le rette OB,
OC, OD, OE, &c. le quali
taglieranno nel medesimo tempo la picciola linea a i anche in otto parti uguali.
Riesce anche questa stessa operazione
per piccola che sia la linea a i, e
per grande che si voglia il numero delle parti. È vero bensì, che volendola
eseguire non potremmo portar molto innanzi la divisione delle parti, poiché le
linee che potremmo tirare dovrebbero sempre aver qualche larghezza, per la
quale verrebbero certamente a confondersi, come Vostra Altezza può vederlo
nella figura vicino al punto O. Ma
quì si tratta di quanto in se stesso è possibile, non già di quanto l’uomo è in
istato di eseguire. Ma nella Geometria le linee non hanno menoma larghezza, e
per conseguenza non si dà mai il caso che si confondano. Adunque ne segue che
una tal divisione non è mai circonscritta da alcuni limiti.
Da che Vostra Altezza mi accorda, che
una linea possa esser divisa in mille parti, con dividere ciascheduna delle
parti in due, verrà questa divisa in duemila parti, e per la stessa ragione in
quattromila, ed in ottomila, senza che giungasi mai alle parti indivisibili.
Per picciola che concepiscasi una linea, certamente questa è divisibile in due
metà, e ciascheduna di queste metà anche in due, e così in infinito.
Quanto finora ho detto di una linea,
si può facilmente applicare ad una superfizie, e con più forte ragione ad un
solido, il quale ha tutte tre le dimensioni, lunghezza, larghezza, profondità.
Da ciò ne nasce, che ogni estensione è divisibile all’infinito, e questa
proprietà chiamasi divisibilità
all’infinito.
Chi volesse negar questa proprietà che
ha l’estensione, sarebbe obbligato a sostenere, che la divisione dovrebbe in
fine ridursi a parti così picciole, che non potrebbero più ulteriormente
dividersi, perché non hanno più estensione. Intanto tutte queste particelle
prese insieme debbon riprodurre quel tutto che fu diviso: e come la quantità di
ciascheduna di esse sarebbe niente o sia zero
0, molti zeri presi insieme dovrebbero produrre una quantità, cosa di cui più
assurda non si può concepire: perché ben sa
Questo sentimento, cioè che nella
divisione di una estensione, o di una quantità qualunque si arriva in fine a
certe particelle tanto picciole, che non sarebber più divisibili, perciocché in
esse non vi sarebbe più quantità, egli è un sentimento assolutamente
insostenibile.
Per renderne più sensibile
l’insussistenza, supponghiamo che una linea di un pollice sia divisa in mille
parti, e che queste sien ridotte a tal picciolezza, che non ammettan più
divisione. Dunque ciascheduna di queste è priva affatto di grandezza (perché se
vi fosse rimasta grandezza, potrebbe ancor dividersi) e per conseguenza
ciascheduna di esse particelle sarebbe un vero niente. Se intanto queste mille
particelle unite insieme formano un pollice, dobbiam dire che un pollice è
composto da mille niente, cosa ch’è tanto assurda, quanto il sostenere, che la metà
di un pollice sia un niente. In fatti se è assurdo l’asserire, che la metà di
una quantità è un niente, lo è eziandìo il dire, che sia un niente il quarto: e
quando ciò mi si accordi riguardo a un quarto, mi si dee accordare anche per la
millesima, e per
Con ragione dunque si asserisce nella
Geometria, che ogni grandezza è divisibile all’infinito, e che in qualunque
divisione non si può mai procedere sino a tal segno, che divenga impossibile
una ulterior divisione. Intanto dee sempre distinguersi ciò ch’è possibile in
se stesso, da ciò che noi siamo in grado di eseguire. La nostra esecuzione ha
molte limitazioni. Dopo aver per esempio diviso un pollice in mille parti, son
queste così picciole che ci sfuggono agli occhi, e perciò ci sarebbe certamente
impossibile una ulterior divisione.
Ma se questa millesima parte di un
pollice si guardasse con un microscopio che ingrandisse per esempio mille
volte, ciascheduna particella ci sembrerebbe altrettanto grande, quanto un
pollice all’occhio nudo: ed in tal caso resterebbe ognuno convinto della
possibilità di divider qualunque di quelle parti in altre mille. Or dunque chi
v’impedisce di tirar sempre innanzi questo stesso raziocinio?
Perlaqualcosa bisogna conchiudere,
ch’egli è questa una verità incontrastabile, che ogni grandezza è divisibile
all’infinito, e non solamente questo ha luogo per l’estensione ch’è oggetto
della Geometria, ma bensì per tutte le altre proprietà, come è il tempo, il
numero &c.” (lettera CXXIII, 28 aprile 1761: II, pp. 191-196).
See moreover:
Si veda inoltre:
Leibniz, G.W. (1734), Essais de Théodicee, I, II, Foppens, Bruxelles.
Euler, L. (1777), Saggio di una difesa della Divina
Rivelazione, Fontana, G. (Ed.) Bolzani, Pavia.
Euler, L. (1787) Institutiones Calculi Differentialis cum
eius usu in Analysi Finitorum ac Doctrina Serierum, I, II, Galeati, Pavia
(II ed.; I ed.: 1755).
Euler, L. (1796), Introduction
a l’Analyse Infinitésimale, I, II, Barrois, Paris (I ed. in French).
Euler, L. (1828), Elements of Algebra, with the notes of M. Bernoulli, &c. and the
additions of M. de La Grange, Longman, Rees, Orme and Co., London.
Syllogismos.it
History and Hermeneutics for Mathematics
Education
(Giorgio T. Bagni, Editor)
Back to Library/Biblioteca
Back to
Syllogismos.it Main Page
Torna a Syllogismos.it
Pagina
Principale