History and Hermeneutics for Mathematics
Education
Storia
ed Ermeneutica per la Didattica della Matematica
La Methode des
Fluxions
by Newton (1740)
Il Metodo delle flussioni di
Newton (1740)
Newton, I. (1740), Le methode des fluxions et des suites infinites, Debure, Paris (I
ed.: 1736)
Problem I. Given x3-ax2+axy-y3 = 0, let us find the ratio of
the fluxions. Example I (La methode des fluxions et des suites infinies, p. 22). Let us replace x
by:
x+
o
and let us replace y by:
y+
o
(being o infinitesimal); so we
obtain:
(x+o)3-a(x+o)2+a(x+o)(y+o)-(y+o)3 = 0
x3+3x2o+3x2o2+3o3-ax2-2axo-a2o2+axy+ayo+axo+ao2-y3-3y2o-3y2o2-3o3
= 0
Let us remember that: x3-ax2+axy-y3 = 0, so it follows:
o(3x2+3x2o+3o2-2ax-a2o+ay+ax+ao-3y2-3y2o-3o2)
= 0
Let us divide and finally put o
equal to zero:
3x2-2ax+ay+ax–3y2 = 0
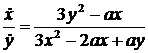
So we have obtained the ratio of the fluxions, as requested.
Problema I.
Data la x3-ax2+axy-y3 = 0,
trovare la relazione delle loro flussioni. Esempio I (La methode des fluxions et
des suites infinies, p. 22). Alla x si sostituisce:
x+o
alla y si sostituisce:
y+o
(essendo o un infinitesimo); otteniamo dunque:
(x+o)3-a(x+o)2+a(x+o)(y+o)-(y+o)3 = 0
x3+3x2o+3x2o2+3o3-ax2-2axo-a2o2+axy+ayo+axo+ao2-y3-3y2o-3y2o2-3o3
= 0
Ricordando che
è: x3-ax2+axy-y3 = 0, si ottiene:
o(3x2+3x2o+3o2-2ax-a2o+ay+ax+ao-3y2-3y2o-3o2)
= 0
Dividiamo per l’infinitesimo
o ed annulliamo infine tale quantità:
3x2-2ax+ay+ax–3y2 = 0
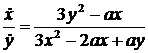
Abbiamo dunque
ricavato il rapporto delle flussioni, come richiesto.
See moreover:
Si veda inoltre:
L’Hospital, G. de (1716), Analyse
des infiniment petits, Papillon, Paris (II ed.).
Riccati,
V. (1752), De
usu motus tractorii in constructione Aequationum Differentialium Commentarius,
Lelio della Volpe, Bologna.
Paulini
a S. Josepho (P. Chelucci) (1755), Institutiones analyticæ earumque usus in
Geometria, Gessari, Napoli.
Newton,
I. (1757), La
cronologia degli antichi regni, Tevernin, Venezia.
Euler,
L. (1787) Institutiones
Calculi Differentialis cum eius usu in Analysi Finitorum ac Doctrina Serierum,
I, II, Galeati, Pavia (II ed.; I ed.: 1755).
Euler,
L. (1796), Introduction
a l’Analyse Infinitésimale, I, II, Barrois, Paris (I ed. in French).
Brunacci,
V. (1804), Corso
di Matematica sublime, I, II, Allegrini, Firenze.
Lagrange, J.L. (1813), Théorie
des fonctions analytiques, Courcier, Paris.
Cauchy, A.L. (1836), Vorlesungen uber die Differenzialrechung,
Meyer, Braunschweig.
Lacroix, S.F. (1837), Traité
elementaire du Calcul Différentiel et du Calcul Intégral, Bachelier, Paris
(V ed.).
De Morgan, A. (1842), The
differential and integral Calculus, Baldwin and Cradock,
Carmichael, R. (1855), A
Treatise on the Calculus of Operations, Longman, Brown, Green and Longmans,
Sturm, Ch. (1868), Cours d’Analyse, I, II,
Gauthier-Villars, Paris.
Carnot, L.N.M. (1881), Réflections
sur la métaphisique du Calcul Infinitésimal, Gauthier-Villars, Paris (I
ed.: 1797).
Laurent, H. (1885-1887-1888), Traité
d’Analyse, I, II, III, Gauthier-Villars, Paris.
Syllogismos.it
History and Hermeneutics for Mathematics
Education
(Giorgio T. Bagni, Editor)
Back to Library/Biblioteca
Back to
Syllogismos.it Main Page
Torna a Syllogismos.it
Pagina
Principale